جدول توزیع نرمال، معمولا برای آزمون فرضیه و مقایسه مقدار بدست آمده آماره با مقادیر موجود در جدول استفاده می شود. پیش از اینکه جدول توزیع نرمال را ملاحظه کنید، توصیه می شود توضیحات زیر را در خصوص متغیرهای تصادفی و توزیع نرمال ملاحظه بفرمایید.
متغیرهای تصادفی
متغیرهای تصادفی دو نوع هستند: گسسته و پیوسته. متغیرهای تصادفی گسسته اساسا وقایع را شمارش میکنند (تعداد خطها در 10 بار پرتاب سکه، تعداد زنان دموکرات ها در یک نمونه و غیره). شناخته شده ترین متغیر تصادفی گسسته متغیرهای با توزیع دوجملهای است. برخلاف متغیر تصادفی گسسته، متغیرهای تصادفی پیوسته وقایع را اندازهگیری میکنند و مقادیر آن میتواند هر عدد حقیقی در بازه مشخصی باشد(زمان لازم برای تکمیل یک کار، نمرات آزمون و غیره). یکی از مهمترین توزیعهای پیوسته توزیع نرمال است که کابرد بسیار وسیعی در علم آمار دارد و اصولا اغلب روشهای آمار استنباطی مبتنی بر این توزیع است.
توزیع نرمال
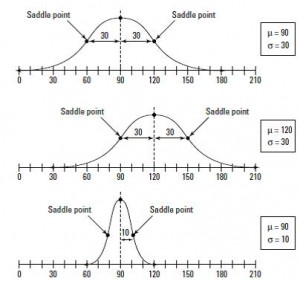
گفته میشود که متغیر تصادفی X دارای توزیع نرمال است است اگر شکل توزیع آن به صورت یک منحنی هموار زنگولهای شکل (متقارن) باشد. منظور از متقارن این است که اگر توزیع را از وسط به دو قسمت تقسیم کنیم هر دو سمت به یک شکل باشند (البته به صورت متقارن نسبت به محور عمودی). هر توزیع نرمال میانگین و انحراف معیار مخصوص به خود را دارد. نمودار زیر توزیع های نرمال با مقادیر مختلف میانگین و انحراف معیار را نشان میدهد. Saddle Point همان نقطه زینی یا نقطه عطف توزیع نرمال است و در واقع نشاندهنده نقطهای است که شکل تابع توزیع احتمال از حالت مقعر به محدب تبدیل میشود.
فاصله میانگین از نقطه زینی در تمامی توزیعهای نرمال همانطور که در نمودار فوق نیز مشاهده می شود برابر یک انحراف معیار است. برای تمامی توزیع های نرمال با میانگین و انحراف معیار مختلف، تمامی مقادیر ممکن تقریبا تا فاصله سه انحراف معیار از میانگین قرار دارند.
توزیع نرمال استاندارد
یکی از مهمترین اعضای خانواده توزیع های نرمال توزیع نرمال استاندارد یا توزیع z است. همه توزیعهای نرمال را می توان به توزیع نرمال استاندارد تبدیل کرد و برای بدست آوردن احتمالات و انجام استنباط آماری استفاده نمود.
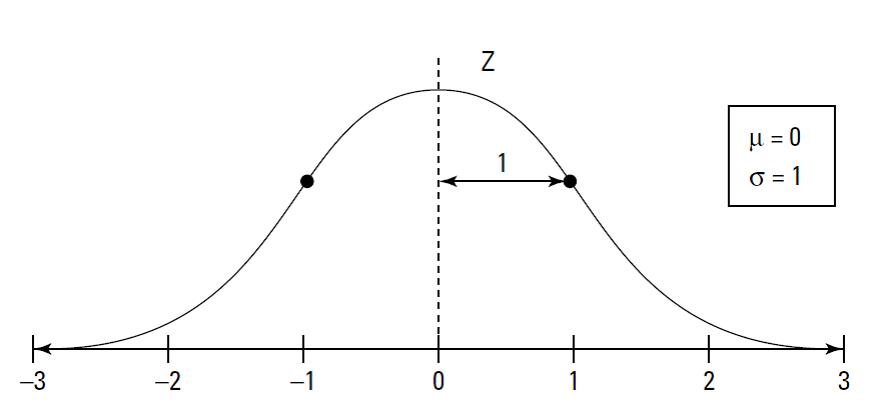
توزیع استاندارد z دارای میانگین صفر و انحراف معیار یک است. شکل این توزیع در زیر آورده شده است. مقادیر توزیع نرمال استاندارد در واقع نشان می دهند که داده مورد بررسی چند انحراف معیار از میانگین فاصله دارد. به عنوان مثال عدد 1 یا -1 در این نمودار نشان دهنده فاصله یک انحراف معیار از میانگین است.
به خاطر فرم تابع توزیع نرمال، محاسبه احتمالات در توزیعهای نرمال به لحاظ محاسبات ریاضی بسیار دشوار است. برای حل این مشکل با استفاده از فرمول زیر تمامی توزیع های نرمال را ابتدا به توزیع نرمال استاندارد تبدیل می کنند و سپس بر اساس جدول منحصر به فردی که برای این توزیع تولید شده است و نشان دهنده احتمالات به ازای مقادیر مختلف است، استنباط آماری را انجام می دهند.
Z=(X-µ)/σ
در رابطه فوق µ میانگین توزیع نرمال مورد نظر و σ انحراف معیار آن است. به عنوان مثال اگر بخواهیم برای توزیعی که دارای میانگین 16 و انحراف معیار 4 است، مقدار معادل عدد 20 را در توزیع استاندارد پیدا کنیم مطابق فرمول فوق میانگین را از عدد 20 کسر کرده (نتیجه 4) و بر انحراف معیار (4) تقسیم می کنیم که نتیجه عدد 1 خواهد بود. به عبارت دیگر عدد 20 ر توزیع نرمال با میانگین 20 و انحراف معیار 4، معادل عدد 1 در توزیع استاندارد است. حال بر اساس جدولی که برای توزیع نرمال استاندارد وجود دارد میتوان احتمالات مربوط به عدد 20 را برای توزیع نرمال محاسبه نمود. شکل زیر جدول مربوط به توزیع نرمال را نشان میدهد
جدول توزیع نرمال
محاسبه مقادیر بحرانی توزیع نرمال
همانطور که در جدول فوق نیز قابل مشاهده است، محاسبه مقادیر احتمالات یا مقادیر بحرانی بر اساس این جدول نیز اندکی مشکل است و گذشته از این بر اساس این جدول نمیتوان مقادیر دقیقی از احتمالات یا مقادیر بحرانی را استخراج نمود. سایت اقتصادیها (سایت تخصصی اقتصاد) این مشکل را برای شما عزیزان رفع کرده و با ابزاری که طراحی و در اختیار شما قرار داده است، محاسبه مقادیر بحرانی و احتمالات را بسیار ساده کرده است.
در ابزار زیر کافی است که سطح احتمال مورد نظر را وارد کنید تا مقدار بحرانی متناظر با آن برای شما تولید شود. در نتایجی که محاسبه می شود بسته به نوع آزمون باید از مقدار بحرانی مختص آن آزمون استفاده کرد. به عبارت دیگر اگر آزمون یک طرفه (از سمت چپ) باشد، از نتایج مربوط به left-tail و اگر آزمون یک طرفه از سمت راست باشد از نتایج قسمت right-tail استفاده می شود. اگر آزمون دو طرفه باشد از نتایج قسمت confidence level استفاده می کنیم. به عنوان مثال در آزمون دوطرفه، مقدار بحرانی متناظر با سطح اطمینان 1.96 است و این عدد در قسمت confidence level نشان داده می شود.
ابزار فوق به ازای هر سطح احتمال مقدار بحرانی متناظر با آن را تولید می کرد، اما ابزار زیر به ازای هر مقدار z، احتمال متناظر با آن را ارائه می دهد. همانند ابزار فوق، این ابزار نیز نتایج را در سه حالت راست دنبله، چپ دنباله و دو طرفه ارائه می کند.













آقا واقعا ممنونم انصافا مطالب آموزنده و کاربردی میذارید خیلی ممنون . از کتابهای کاربردی و فیلمهای آموزشی هم غافل نشید و ما رو هم بی بهره نذارید . تشکر
این ابزاری که گذاشتین خیلی خوبه ولی شما باید طریقه پیدا کردن خود عدد را هم توضیح بدین ،
بسم الله…
واقعا ممنون بابت توضیح روان و کاملتون.بسیار عالی بود.انصافا زکات علمتون رو پرداخت کردین….
واقعا مطالبتون عالی و کاربردی هستش عالییییییییییییی