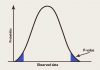
ویژگی های توزیع نرمال
ویژگی های توزیع نرمال که یکی از رایج ترین توزیع های آماری به شمار می رود، عبارتند از:
- توزیع نرمال حول میانگین متقارن بوده و زنگوله ای شکل است. این ویژگی باعث می شود که 50 درصد از سطح زیر منجنی در یک سمت زنگوله و 50 درصد دیگر در سمت دیگر زنگوله قرار گیرد. همچنین این ویژگی به این معنی است که پیشامدهایی که به یک اندازه از میانگین (به عنوان مثال یک انحراف معیار، پایین تر از میانگین و یک انحراف معیار بالاتر از میانگین) فاصله دارند، دارای احتمال وقوع یکسانی باشند.
P(-σ<x<μ)=P(μ<x<σ)
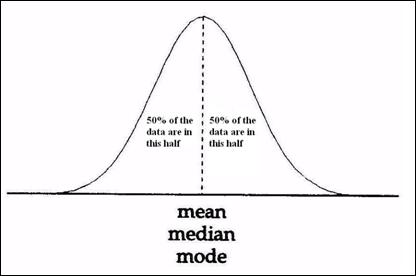
- میانگین، میانه و مد در توزیع نرمال با هم برابر هستند.
- مشتق مرتبه اول توزیع برای مقادیر کوچکتر از میانگین (x<μ)، مثبت و برای مقادیر بزرگتر از میانگین (x>μ)، منفی است. همچنین مشتق مرتبه اول توزیع در نقطه میانگین (x=μ) برابر صفر است.
- سطح زیر منحنی در طول محور x، مجموعا برابر یک است.
- مقدار چولگی توزیع نرمال برابر صفر است. زمانی که توزیع متقارن است، چولگی برابر صفر است.
- مقدار کشیدگی اضافی توزیع نرمال برابر صفر است. کشیدگی اضافی از کسر کردن عدد 3 از مقدار کشیدگی به دست میآید. بر این اساس، مقدار کشیدگی توزیع نرمال برابر 3 است که با کسر عدد 3، کشیدگی اضافی آن، برابر صفر می شود.
- توزیع نرمال دارای دو نقطه عطف در نقاط x+σ و x-σ است. در واقع در این دو نقطه مقدار مشتق مرتبه دوم، برابر صفر بوده و مشتق مرتبه دوم در این نقطه تغییر علامت می دهد.
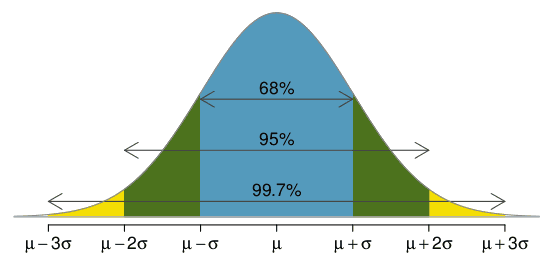
- با دور شدن از میانگین به اندازه چند انحراف معیار، مقدار توزیع نرمال تقریبا به صفر میل می کند. سطح زیر منحنی بعد از سه انحراف معیار، تقریبا برابر 0.27 درصد کل سطح زیر منحنی است.
- سطح زیر منحنی در بازه یک انحراف معیار تقریبا 68 درصد، در بازه دو انحراف معیار 95 درصد و در بازه سه انحراف معیار برابر 99.73 درصد است
- گشتاورهای مرکزی توزیع نرمال با مرتبه فرد، برابر صفر هستند. گشتاورهای مرکزی توزیع نرمال از طریق فرمول زیر قابل محاسبه هستند:

در فرمول فوق، علامت !! نشان دهنده دو بار عملیات فاکتوریل است. بر اساس فرمول فوق گشتاورهای توزیع نرمال به شکل زیر محاسبه می شوند.
| مرتبه | گشتاور غیر مرکزی | گشتاور مرکزی |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
رابطه توزیع نرمال با سایر توزیع ها
- زمانی که درجه آزادی توزیع t افزایش می یابد، توزیع t به توزیع نرمال با میانگین صفر و واریانس یک میل می کند.
- توزیع دو جمله ای (B(n,p به ازای n های بزرگ و p هایی که باه مقادیر حدی صفر و یک زیاد نزدیک نیستند، به توزیع نرمال میل می کند که دارای میانگین np و واریانس (np(1-p است.
- توزیع پواسون زمانی که λ یک عدد نسبتا بزرگی است، به توزیع نرمال با میانگین λ و واریانس λ میل می کند.
- توزیع کای دو با k درجه آزادی، زمانی که k عدد بزرگی است به توزیع نرمال با میانگین k و واریانس 2k میل می کند.
برای مطالعه توضیحات بیشتر در خصوص توزیع نرمال و جدول توزیع نرمال به این صفحه مراجعه کنید.