فروض رگرسیون یا فروض کلاسیک رگرسیون
رگرسیون برای اینکه نتایج مورد انتظار ما را بدست دهد و به عبارت دیگر تخمین زننده پارامترهای مدل، دارای حداقل واریانس بوده و بدون تورش باشند، یک سری فروض بر رگرسیون اعمال می شود که به فروض رگرسیون یا فروض کلاسیک رگرسیون شهرت دارند. چون برخی از فروض روش OLS مربوط به حالت چند متغیره میباشد بنابراین، قبل از عنوان نمودن فروض روش OLS ابتدا به معرفی روش رگرسیونی چند متغیره پرداخته میشود. در حالت کلی رگرسیون چند متغیره را میتوان به سادگی به شکل ماتریسی نشان داد.
![]() ,
, ![]() 5)
5)
یا

یا Y=XB+U
که در آن X نمایانگر ماتریس متغیرهای توضیحی میباشد که هر ستون آن مربوط به مشاهدات یکی از متغیرهای توضیحی میباشد. ماتریس B نیز شامل ضرایب متغیرهای توضیحی بوده و k نشاندهنده تعداد متغیرهای توضیحی میباشد. Y و U نیز به ترتیب نمایانگر بردار متغیر توضیحی و بردار جملات اخلات اخلال میباشند.
پس از مقدمه ای که در مورد رگرسیون چند متغیره آورده شد در اینجا به توضیح فروض اصلی روش OLS پرداخته میشود:
خطی بودن مدل رگرسیونی نسبت به پارامترها:
یکی از فروض رگرسیون یا به عبارت بهتر، اولین مورد از فروض کلاسیک رگرسیون بیان می کند که در روش OLS باید مدل رگرسیونی نسبت به پارامترها( ![]() ) خطی باشد. باید به این نکته توجه شود که این خطی بودن صرفا نسبت به پارامترها میباشد و نیازی نیست که مدل رگرسیونی نسبت به متغیرهای توضیحی خطی باشد. به عنوان مثال، معادلات عنوان شده در قسمت (الف) معادلات خطی بوده ولی معادلات آورده شده در قسمت (ب) معادلات غیرخطی نسبت به پارامترهای میباشند:
) خطی باشد. باید به این نکته توجه شود که این خطی بودن صرفا نسبت به پارامترها میباشد و نیازی نیست که مدل رگرسیونی نسبت به متغیرهای توضیحی خطی باشد. به عنوان مثال، معادلات عنوان شده در قسمت (الف) معادلات خطی بوده ولی معادلات آورده شده در قسمت (ب) معادلات غیرخطی نسبت به پارامترهای میباشند:
الف)  ب)
ب) 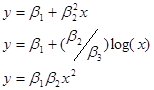
نمونه ای که در روش OLS به کار میرود باید شامل سه ویژگی زیر باشد:
1-نمونه باید شامل n جفت مشاهده باشد که به صورت کاملا تصادفی از جامعه استخراج شده است.
2-تعداد مشاهدات باید بزرگتر از تعداد پارامترها باشد(n>k).
در صورتی که تعداد مشاهدات برابر تعداد پارامترها باشد( n=k) در این صورت دیگر نیازی به برآورد پارامترها وجود ندارد چرا که معادله رگرسیونی به یک دستگاه معادلات با تعداد مجهولات و معلومات برابر تقلیل مییابد و با استفاده از شیوههای معمول حل دستگاه معادلات قابل حل است. همچنین اگر تعداد مشاهدات کمتر از تعداد پارامترها باشد(n<k) امکان برآورد پارامترها میسر نمیباشد، چون تعداد مجهولات(پارامترها) بیشتر از تعداد معلومات(مشاهدات) میباشد.
3- متغیرهای توضیحی، متغیرهای غیرتصادفی هستند[1] که مقادیر آنها ثابت میباشد.
این فرض بیان میکند که رابطه علی بین متغیرهای توضیحی و متغیر وابسته یک رابطهی علی یک طرفه میباشد. به عبارت دیگر تغییر در متغیرهای توضیحی سبب تغییر در متغیر وابسته میشود(متغیرهای توضیحی علت متغیر وابسته هستند) اما تغییر در متغیر وابسته سبب تغییر در متغیرهای توضیحی نمیشود(متغیر وابسته علت متغیرهای توضیحی نمیباشد). این فرض همچنین مشخص میکند که تصادفی بودن y ها تنها ناشی از تصادفی بودن جملات اخلال میباشد چرا که فرض میشود که x ها غیرتصادفی هستند[2].
صفر بودن میانگین شرطی جملات اخلال:
یکی دیگر از فروض رگرسیون این است که امید ریاضی جملات اخلال به ازای هر یک از مقادیر X برابر صفر میباشد. این فرض را میتوان به شکل ریاضی به صورت زیر نوشت:
![]() 6)
6)
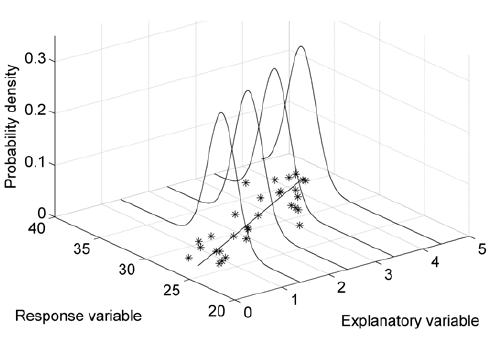
این فرض بیان میکند که توزیع مربوط به جملات اخلال به ازای هر مقدار X، توزیعی میباشد که دارای میانگین صفر است. این فرض به صورت نموداری به شکل زیر قابل بیان است.

دو نتیجه مهم که از این فرض حاصل میشود این است که 1) ![]() است و همچنین 2)
است و همچنین 2) ![]() می باشد. مفهوم این دو این است که میانگین غیر شرطی U نیز برابر صفر بوده و نیز کواریانس میان متغیرهای توضیحی و جملات اخلال برابر صفر میباشد.
می باشد. مفهوم این دو این است که میانگین غیر شرطی U نیز برابر صفر بوده و نیز کواریانس میان متغیرهای توضیحی و جملات اخلال برابر صفر میباشد.
نتیجه ی اول به راحتی از قانون امید ریاضی تکراری[3] قابل حصول است. بر طبق این قانون رابطه ی زیر برقرار است:
![]() 7)
7)
اگر از قانون فوق در رابطهی (6) استفاده شود، نتیجهی E(U)=0 حاصل خواهد شد:
![]() 8)
8)
با به کارگیری نتیجه اول و با تکیه بر این فرض که متغیرهای توضیحی(X) مقادیر ثابتی هستند، میتوان صحت نتیجه دوم را نیز نشان داد:
![]() 9)
9)
بر طبق قانون امید ریاضی تکراری خواهیم داشت:
![]() 10)
10)
بر طبق نتیجه یک(رابطه 8)، داریم:
![]() 11)
11)
و چون کواریانس دو متغیر برابر است با: ![]() میتوان نتیجه گرفت که کواریانس جملات اخلال با متغیرهای توضیحی برابر با صفر است.
میتوان نتیجه گرفت که کواریانس جملات اخلال با متغیرهای توضیحی برابر با صفر است.
عدم وجود همخطی :
یکی از فروض کلاسیک رگرسیون خطی این است که هیچگونه همخطی مرکب بین متغیرهای توضیحی موجود در مدل وجود ندارد. این فرض دارای دو مفهوم است: اول اینکه هیچ متغیر دیگری به جز عرض از مبدا نمیتواند مقادیر ثابتی داشته باشد و دوم اینکه متغیرها باید تا حدود زیادی متفاوت از هم باشند و تغیراتشان زیاد باشد. همخطی تنها ارتباطات خطی بین متغیرهای X را شامل میشود و ارتباطات غیرخطی بین آنها را در بر نمیگیرد.
همسانی واریانس:
یکی از مهمترین فروض رگرسیون خطی کلاسیک این است که اجزاء اخلال U که در تابع رگرسیون جامعه ظاهر میشوند، دارای واریانس همسان هستند. این فرض به صورت نموداری و جبری توضیح داده شده است.

الف) واریانسهای همسان

ب) واریانسهای ناهمسان
نمایش جبری واریانس همسانی نیز به شکل زیر میباشد:
![]() 12)
12)
عدم وجود خود همبستگی:
یکی از فروض مهم دیگر از فروض کلاسیک رگرسیون این است که خودهمبستگی سریالی بین اجزاء اخلالی که در تابع رگرسیون جامعه وارد میشود وجود ندارد. به عبارت دیگر:
![]() 13)
13)
قسمت (الف) نمودار زیر نشاندهنده حالتی است که خود همبستگی وجود دارد، قسمت (ب) نیز نمایانگر حالتی است که خود همبستگی وجود ندارد.
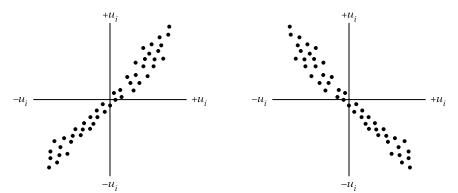
الف) وجود خود همبستگی
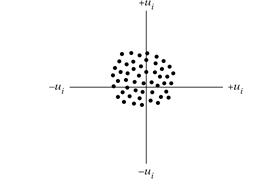
ب) عدم وجود خود همبستگی
عدم وجود خطای تصریح:
یکی دیگر از فروض کلاسیک رگرسیون عدم وجود خطای تصریح در مدل است. یک تحقیق اقتصاد سنجی با تصریح مدل آن، در رابط با پدیدههای مشاهده شده مورد نظر آغاز میشود. برخی از مهمترین سوالات مطرح شده در رابطه با تصریح مدل عبارتند از:
1-چه متغیرهایی باید در مدل جای گیرند؟
2-شکل تابعی مدل چگونه است؟
3-آیا مدل از نظر متغیرها و/ یا پارامترها خطی است؟
4-فرضهای احتمالی ارائه شده در مورد متغیرهای وابسته، متغیر مستقل و جمله اخلال درون مدل چه میباشند؟
نرمال بودن توزیع جملات اخلال
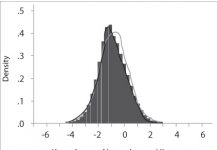
نرمال بودن توزیع جملات اخلال نیز آخرین مورد از فروض رگرسیون یا همان فروض کلاسیک رگرسیون است. اگر هدف ما تنها تخمین پارامترها باشد در اینصورت روش OLS کافی خواهد بود اما تأکید بر تخمین تنها یکی از جنبههای استنتاج آماری است و جنبۀ دیگر آزمون فرضیه میباشد. از آنجا که هدفمان هم تخمین پارامترها و هم آزمون فرضیه است، لذا احتیاج به تعیین توزیع احتمالی جزء اخلال ui خواهیم داشت، بنابراین فرض می کنیم که جملات اخلال دارای توزیع نرمال با میانگین صفر و واریانس ثابت باشد.
13) ![]()
این فرض علاوه بر اینکه در انجام آزمون فرضیه نقش ایفا میکند سبب میشود تا برآوردهای انجام شده از طریق OLS منطبق با برآوردهای روش حداکثر راستنمایی[4] شود و بنابراین موجب میشود تا روش OLS به صورت مجانبی کاراترین[5] روش در میان تخمین زننده های معمول باشد.
البته باید توجه داشت، در صورتی که تعداد داده های نمونه مورد بررسی به اندازه کافی بزرگ باشد و فروض همسانی واریانس، عدم وجود خود همبستگی و صفر بودن میانگین جملات اخلال برقرار باشد، بر طبق قضیه حد مرکزی[6] انتظار بر این است که توزیع جملات اخلال یک توزیع نرمال باشد.
[1] . اگر x ها با وجود تصادفی بودن به طور مستقل از u ها توزیع شوند آنگاه برای تمام مقاصد کاربردی، xها را میتوان غیرتصادفی فرض کرد.
[2] .چرا که تنها دو عامل سبب تعیین y میشود: متغیرهای توضیحی و جملات اخلال. از آنجا که x ها غیر تصادفی هستند بنابراین تصادفی بودن y ها تنها میتواند ناشی از تصادفی بودن جملات اخلال باشد.
[3] . Iterated expectation
[4] .Maximum Likelihood
[5] .Asymptotically Efficient
[6] .Central Limit Theorem
[list icon=”momizat-icon-pencil2″ icon_color=”#1e73be” icon_color_hover=”#dd3333″ icon_bg=”circle” ]مقاله قبلی[/list]
[box type=”info” radius=”5″]
حداقل مربعات معمولی (روش OLS)
[/box]