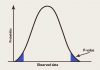
حداقل مربعات معمولی (روش OLS)
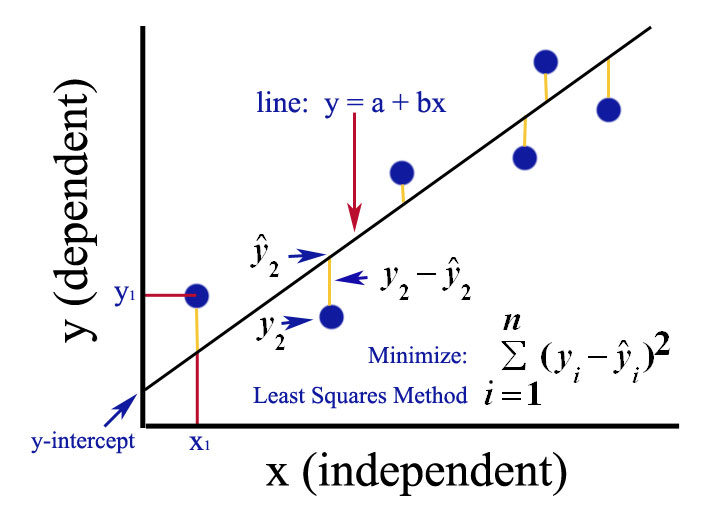
از میان روشهای مختلف خطی[3] برای برآورد پارامترهای مدل( ![]() ) روش OLS[4] یا همان حداقل مربعات معمولی به خاطر خواص مطلوبی(البته هنگامی که فروض این روش برقرار باشند) که دارد به عنوان پرکاربردترین و غالبترین روش شناخته شده است. این روش که به کارل فردریک گوس، ریاضیدان نامی آلمان نسبت داده میشود از طریق حداقل کردن مجموع مربعات جملات اخلال[5] تلاش میکند که بهترین خط رگرسیونی برای دادهها را برازش نماید.
) روش OLS[4] یا همان حداقل مربعات معمولی به خاطر خواص مطلوبی(البته هنگامی که فروض این روش برقرار باشند) که دارد به عنوان پرکاربردترین و غالبترین روش شناخته شده است. این روش که به کارل فردریک گوس، ریاضیدان نامی آلمان نسبت داده میشود از طریق حداقل کردن مجموع مربعات جملات اخلال[5] تلاش میکند که بهترین خط رگرسیونی برای دادهها را برازش نماید.
![]() 2)
2)
بنابراین روش OLS سعی دارد تا رابطه شماره (3) را حداقل نماید:
![]() 3)
3)
با حداقل کردن رابطه شماره (3) روش OLS برآوردهایی از پارامترها را ارائه مینماید که با رابطهی زیر قابل محاسبه است:
4) 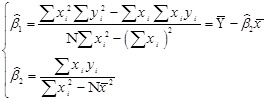
اگر هدف ما تنها تخمین ![]() و
و ![]() باشد، روش OLS کافی است اما در تحلیل رگرسیون هدف تنها بدستآوردن برآوردهایی از
باشد، روش OLS کافی است اما در تحلیل رگرسیون هدف تنها بدستآوردن برآوردهایی از ![]() و
و ![]() نیست بلکه هدف استنتاجاتی دربارۀ
نیست بلکه هدف استنتاجاتی دربارۀ ![]() و
و ![]() واقعی میباشد. برای رسیدن به این هدف نه تنها باید شکل تبعی مدل را تعیین کنیم بلکه باید فرضیات معینی دربارۀ چگونگی بوجودآمدن
واقعی میباشد. برای رسیدن به این هدف نه تنها باید شکل تبعی مدل را تعیین کنیم بلکه باید فرضیات معینی دربارۀ چگونگی بوجودآمدن ![]() و
و ![]() را نیز مطرح سازیم:
را نیز مطرح سازیم:
معادله (1) نشان میدهد که ![]() هم به
هم به ![]() و هم به
و هم به ![]() بستگی دارد. بنابراین تا زمانی که ندانیم
بستگی دارد. بنابراین تا زمانی که ندانیم ![]() و
و ![]() چگونه بدست میآیند هیچ راهی برای دستیابی به استنتاجات آماری دربارۀ
چگونه بدست میآیند هیچ راهی برای دستیابی به استنتاجات آماری دربارۀ ![]() و همچنین
و همچنین ![]() و
و ![]() نخواهیم داشت. از این رو فرضیات مبتنی بر متغیرهای توضیحی و جزء خطا برای تفسیر معتبری از تخمینهای رگرسیون اهمیت دارند.
نخواهیم داشت. از این رو فرضیات مبتنی بر متغیرهای توضیحی و جزء خطا برای تفسیر معتبری از تخمینهای رگرسیون اهمیت دارند.
[1] .Stochastic
[2] .Occam’s razor
[3] از آنجا که در روش OLS (حداقل مربعات معمولی)، پارامترهای تخمین زده شده یه صورت ترکیب خطی از ![]() هستند به همین خاطر روش OLS یک روش خطی نامیده میشود. برای نشان دادن اینکه پارامترهای تخمین زده شده ترکیب خطی از متغیر وابسته هستند، کافیست متغیر
هستند به همین خاطر روش OLS یک روش خطی نامیده میشود. برای نشان دادن اینکه پارامترهای تخمین زده شده ترکیب خطی از متغیر وابسته هستند، کافیست متغیر ![]() را به صورت زیر تعریف کنیم:
را به صورت زیر تعریف کنیم:
![]()
در این صورت ![]() برابر خواهد بود با:
برابر خواهد بود با:
![]()
که ترکیب خطی از ![]() میباشد.
میباشد.
[4] .Ordinary Least Squares
[5] . روش OLS از مربعات جملات اخلال استفاده میکند. این بدین معناست که در روش OLS خطاهای بزرگتر بیشتر جریمه میشوند.
[list icon=”momizat-icon-pencil2″ icon_color=”#1e73be” icon_color_hover=”#dd3333″ icon_bg=”circle” ]مقاله قبلی[/list]
[box type=”info” radius=”5″]
رگرسیون چیست؟ (تاریخچه و مفهوم)
[/box]
[list icon=”momizat-icon-pencil2″ icon_color=”#1e73be” icon_color_hover=”#dd3333″ icon_bg=”circle” ]مقاله بعدی[/list]
[box type=”info” radius=”5″]
فروض رگرسیون (فروض کلاسیک رگرسیون)
[/box]